let's check this video dengan cara klik link dibawah ini
https://www.youtube.com/watch?v=ZJ5Y4BDYcjQ
dari video diatas mari kita bahas tentang hiperboloida
jadi Hiperboloida adalah himpunan titik-titik di dim
ensi tiga yang selisih jaraknya terhadap dua titik tetap yang disebut titik fokus adalah sama. Hiperboloida dibagi menjadi dua, yaitu hiperboloida satu daun (one sheet) dan hiperboloida dua dauh ( two sheet).
Selasa, 28 Mei 2019
LAPORAN TUGAS UAS GEOMETRI ANALITIK
https://drive.google.com/file/d/12lTvtFyn7VO_if5wCk1HwO15f8i_IdSl/view?usp=sharing
Selasa, 21 Mei 2019
Hiperbola
sebelum membaca postingan tentang hiperbola mari simak terlebih dahulu video berikut dengan cek link di bawah
let's check this out
https://youtu.be/ZtRXuo4GpWg
https://www.youtube.com/watch?v=ZtRXuo4GpWg
mari kita bahas
Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola.
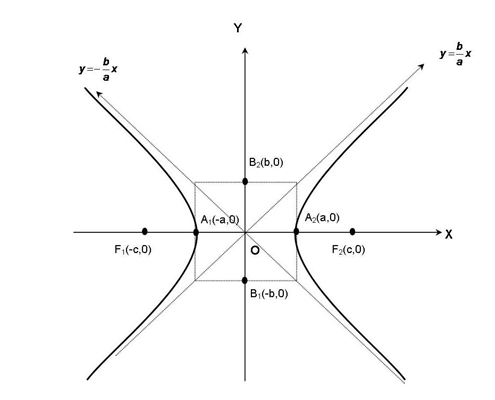
Gambar tersebut merupakan hiperbola yang berpusat di titik O(0,0).
• F1( -c, 0) dan F2(c, 0) adalah titik fokus hiperbola yang jaraknya 2c. Sementara selisih jarak yang tetap itu adalah 2a.
• Sumbu utama adalah sumbu x, sedangkan sumbu sekawan adalah sumbu y.
• Sumbu mayor adalah A1A2, panjangnya 2a. Sumbu minor adalah B1B2, panjangnya 2b.
• Titik A1 dan A2 disebut titik puncak hiperbola yang merupakan titik potong hiperbola dengan sumbu mayor.
• Lactus rectum adalah garis vertikal yang melalui salah satu fokus, tegak lurus sumbu mayor, dan memotong hiperbola di dua titik. Panjang lactus rektum adalah
2b2a
Persamaan asimtot hiperbola adalah
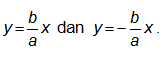 • Eksentrisitas = e = c/a , dengan e > 1.
• Eksentrisitas = e = c/a , dengan e > 1.
• Persamaan garis direktriks adalah
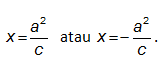 • Ketentuan khusus pada hiperbola yaitu c2 = a2 + b2.
• Ketentuan khusus pada hiperbola yaitu c2 = a2 + b2.
 Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu x adalah
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu x adalah
x2a2 − y2b2 = 1
Titik fokus adalah F1(c, 0) dan F2(-c, 0).
Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah
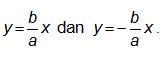 Bagaimana jika sumbu utamanya adalah sumbu y?
Bagaimana jika sumbu utamanya adalah sumbu y?
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah
y2a2 − x2b2 = 1
Titik fokus adalah F1(0, c) dan F2(0, -c).
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah
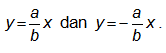 Agar kamu lebih paham, coba cermati contoh soal berikut.
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 1:
Tentukan persaman asimtot dari persamaan
x29−y216=1
Penyelesaian:
Coba perhatikan bahwa sumbu utama persamaan hiperbola ini adalah sumbu x. Akibatnya, a2 = 9 dan b2 = 16, sehingga a = 3 dan b = 4.
Persamaan asimtotnya adalah
 b. Persamaan hiperbola yang berpusat di titik (p, q)
b. Persamaan hiperbola yang berpusat di titik (p, q)
 Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utamanya sejajar dengan sumbu x adalah
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utamanya sejajar dengan sumbu x adalah
(x − p)2a2 − (y − q)2b2 = 1
Titik fokus adalah F1(p + c, q) dan F2(p – c, q).
Titik puncak adalah A1(p + a, q) dan A2(p – a, q).
Persamaan asimtotnya adalah
 Bagaimana jika sumbu utama hiperbola sejajar dengan sumbu y?
Bagaimana jika sumbu utama hiperbola sejajar dengan sumbu y?
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utama sejajar dengan sumbu y adalah
(y − q)2a2 − (x − p)2b2 = 1
Titik fokus adalah F1(p, q + c) dan F2(p, q – c).
Titik puncak adalah A1(p, q + a) dan A2(p, q – a).
Persamaan asimtotnya adalah
 Agar kamu lebih paham, coba cermati contoh soal berikut.
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 2:
Sebuah hiperbola mempunyai persamaan 9x2 – 4y2 – 36x – 8y + 68 = 0.
Tentukan titik pusat, titik puncak, dan titik fokus hiperbola tersebut!
Penyelesaian:
Ayo, ubah bentuk persamaan tersebut ke dalam bentuk baku.
9x2 – 4y2 – 36x – 8y + 68 = 0
9x2 – 36x – 4y2 – 8y = –68
9(x2 – 4x + 4) – 4(y2 + 2y + 1) = –68 + 36 – 4
9(x – 2)2 – 4(y + 1)2 = –36
4(y + 1)2 – 9(x – 2)2 = 36
(y + 1)29 − (x − 2)24 = 1
Persamaan hiperbola ini memiliki sumbu utama yang sejajar dengan sumbu y dengan a2 = 9 dan b2 = 4. Akibatnya, c2 = a2 + b2 = 9 + 4 = 13.
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah

 Pada gambar tersebut garis g menyinggung hiperbola pada titik R(x1, y1).
Pada gambar tersebut garis g menyinggung hiperbola pada titik R(x1, y1).
a. Persamaan garis singgung yang melalui suatu titik pada hiperbola
• Persamaan garis singgung pada suatu titik R(x1, y1) pada hiperbola
x2a2 − y2b2 = 1
adalah
x1xa2 − y1yb2 = 1
 Agar kamu lebih paham, coba cermati contoh soal berikut.
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 3:
Coba tentukan persamaan garis singgung pada titik (9, 2) yang terletak pada hiperbola
(y + 2)248 − (x − 5)212 = 1
Penyelesaian:
Persamaan garis singgungnya dapat dihitung seperti berikut.
(y 1− q)(y − q)a2 − (x1 − p)(x − p)b2= 1(2+ 2)(y + 2)48 − (9 − 5)(x − 5)12= 1(y + 2)12 − (x − 5)3= 1
y – 4x + 10 = 0
Jadi, persamaan garis singgungnya adalah y – 4x + 10 = 0.
b. Persamaan garis singgung bergradien m pada hiperbola
Misalkan garis g yang menyinggung hiperbola tersebut bergradien m, maka:

x2100−y264=1
let's check this out
https://youtu.be/ZtRXuo4GpWg
https://www.youtube.com/watch?v=ZtRXuo4GpWg
mari kita bahas
Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola.
Gambar tersebut merupakan hiperbola yang berpusat di titik O(0,0).
• F1( -c, 0) dan F2(c, 0) adalah titik fokus hiperbola yang jaraknya 2c. Sementara selisih jarak yang tetap itu adalah 2a.
• Sumbu utama adalah sumbu x, sedangkan sumbu sekawan adalah sumbu y.
• Sumbu mayor adalah A1A2, panjangnya 2a. Sumbu minor adalah B1B2, panjangnya 2b.
• Titik A1 dan A2 disebut titik puncak hiperbola yang merupakan titik potong hiperbola dengan sumbu mayor.
• Lactus rectum adalah garis vertikal yang melalui salah satu fokus, tegak lurus sumbu mayor, dan memotong hiperbola di dua titik. Panjang lactus rektum adalah
Persamaan asimtot hiperbola adalah
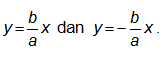
• Persamaan garis direktriks adalah
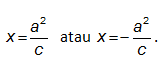
- Persamaan Hiperbola a. Persamaan hiperbola yang berpusat di titik (0, 0)

Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah
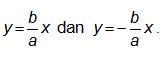
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah
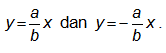
Contoh 1:
Tentukan persaman asimtot dari persamaan
Coba perhatikan bahwa sumbu utama persamaan hiperbola ini adalah sumbu x. Akibatnya, a2 = 9 dan b2 = 16, sehingga a = 3 dan b = 4.
Persamaan asimtotnya adalah


Titik puncak adalah A1(p + a, q) dan A2(p – a, q).
Persamaan asimtotnya adalah

Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utama sejajar dengan sumbu y adalah
Titik puncak adalah A1(p, q + a) dan A2(p, q – a).
Persamaan asimtotnya adalah

Contoh 2:
Sebuah hiperbola mempunyai persamaan 9x2 – 4y2 – 36x – 8y + 68 = 0.
Tentukan titik pusat, titik puncak, dan titik fokus hiperbola tersebut!
Penyelesaian:
Ayo, ubah bentuk persamaan tersebut ke dalam bentuk baku.
9x2 – 4y2 – 36x – 8y + 68 = 0
9x2 – 36x – 4y2 – 8y = –68
9(x2 – 4x + 4) – 4(y2 + 2y + 1) = –68 + 36 – 4
9(x – 2)2 – 4(y + 1)2 = –36
4(y + 1)2 – 9(x – 2)2 = 36
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah

- Persamaan Garis Singgung Hiperbola Sebuah garis digambarkan pada sebuah hiperbola. Salah satu kedudukan yang mungkin antara garis itu dan hiperbola adalah garis menyinggung hiperbola. Coba perhatikan gambar berikut.

a. Persamaan garis singgung yang melalui suatu titik pada hiperbola
• Persamaan garis singgung pada suatu titik R(x1, y1) pada hiperbola

Contoh 3:
Coba tentukan persamaan garis singgung pada titik (9, 2) yang terletak pada hiperbola
Persamaan garis singgungnya dapat dihitung seperti berikut.
Jadi, persamaan garis singgungnya adalah y – 4x + 10 = 0.
b. Persamaan garis singgung bergradien m pada hiperbola
Misalkan garis g yang menyinggung hiperbola tersebut bergradien m, maka:

Langganan:
Komentar (Atom)

